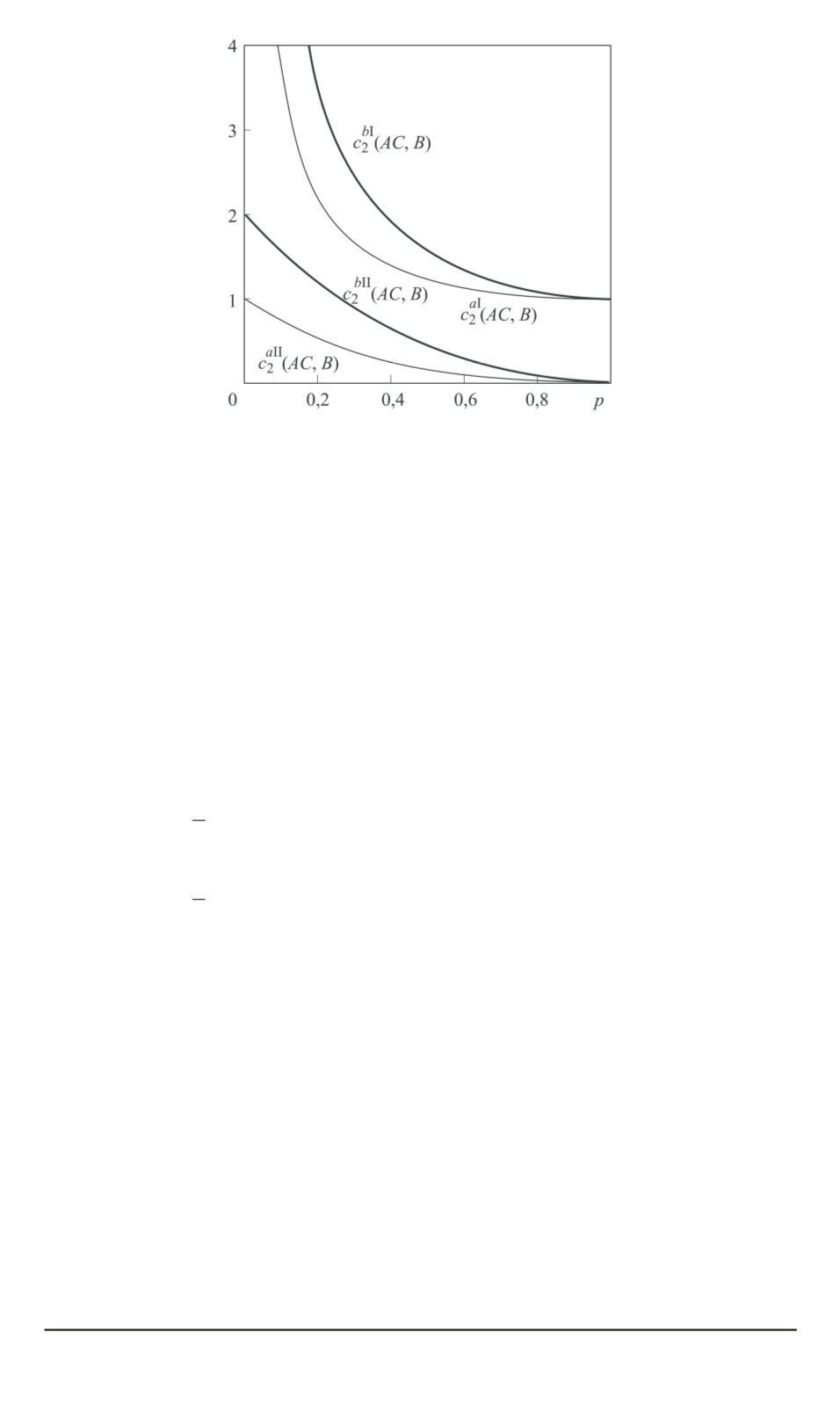
Рис. 4. Поведение причинностей в звене
AC
,
B
при различных конфигурациях
эксперимента
Алисы. Таким образом, с формальной позиции причинного анализа
возможно получить ситуацию, когда причина идет за следствием.
Рассмотрим те же четыре случая с позиции обратно-временн ´ого
подхода. Введем новый объект, который обозначим буквой
D
, являю-
щийся результатом белловского измерения
A
и
C
. Кроме того, согласно
обратно-временн´ому подходу не существует различий конфигураций
a
и
b
. В конечном счете можно записать две “матрицы плотности”
для вариантов I и II (верхний индекс “tr” указывает на использование
обратно-временн´ого формализма)
ρ
I
,
tr
ACBD
=
1
4
4
X
j
=1
0
, W
j
0
, W
†
4
W
j
0
,
Ψ
j
ED
0
, W
j
0
, W
†
4
W
j
0
,
Ψ
j
;
ρ
II
,
tr
ACBD
=
1
8
X
i
=0
,
1
4
X
j
=1
i, W
j
i, W
†
4
W
j
i,
Ψ
j
ED
i, W
j
i, W
†
4
W
j
i,
Ψ
j
.
(3)
Для состояний (3) имеем следующие результаты:
c
I
,
tr
2
(
AC, B
) =
∞
,
c
I
,
tr
2
(
D, B
) = 1
— эти значения соответствуют случаям
a
I и
b
I при
p
= 0
и
p
= 1
;
c
II
,
tr
2
(
AC, B
) = 1
,
c
II
,
tr
2
(
D, B
) = 0
— эти значения соответ-
ствуют случаям
a
II при
p
= 0
, а также
a
II и
b
II при
p
= 1
(см.
рис. 3). Отметим, что получили
c
b
II
2
(
AC, B
) = 2
при
p
= 0
, так как
S
(
CB
) = 0
. В случае обратно-временн´ого подхода всегда
S
(
CB
) = 1
,
поскольку состояние “знает”, что оно будет измерено.
В рамках обратно-временн´ого подхода можно рассмотреть два но-
вых звена:
AD, C
и
AD, B
. Из (3) находим
c
I
,
tr
2
(
AD, C
) =
c
I
,
tr
2
(
AD, B
) =
= 1
и
c
II
,
tr
2
(
AD, C
) =
c
II
,
tr
2
(
AD, B
) = 1
/
2
. Эти значения описыва-
ют распространение кубита через обратное время, т.е. в обратно-
32
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 6


