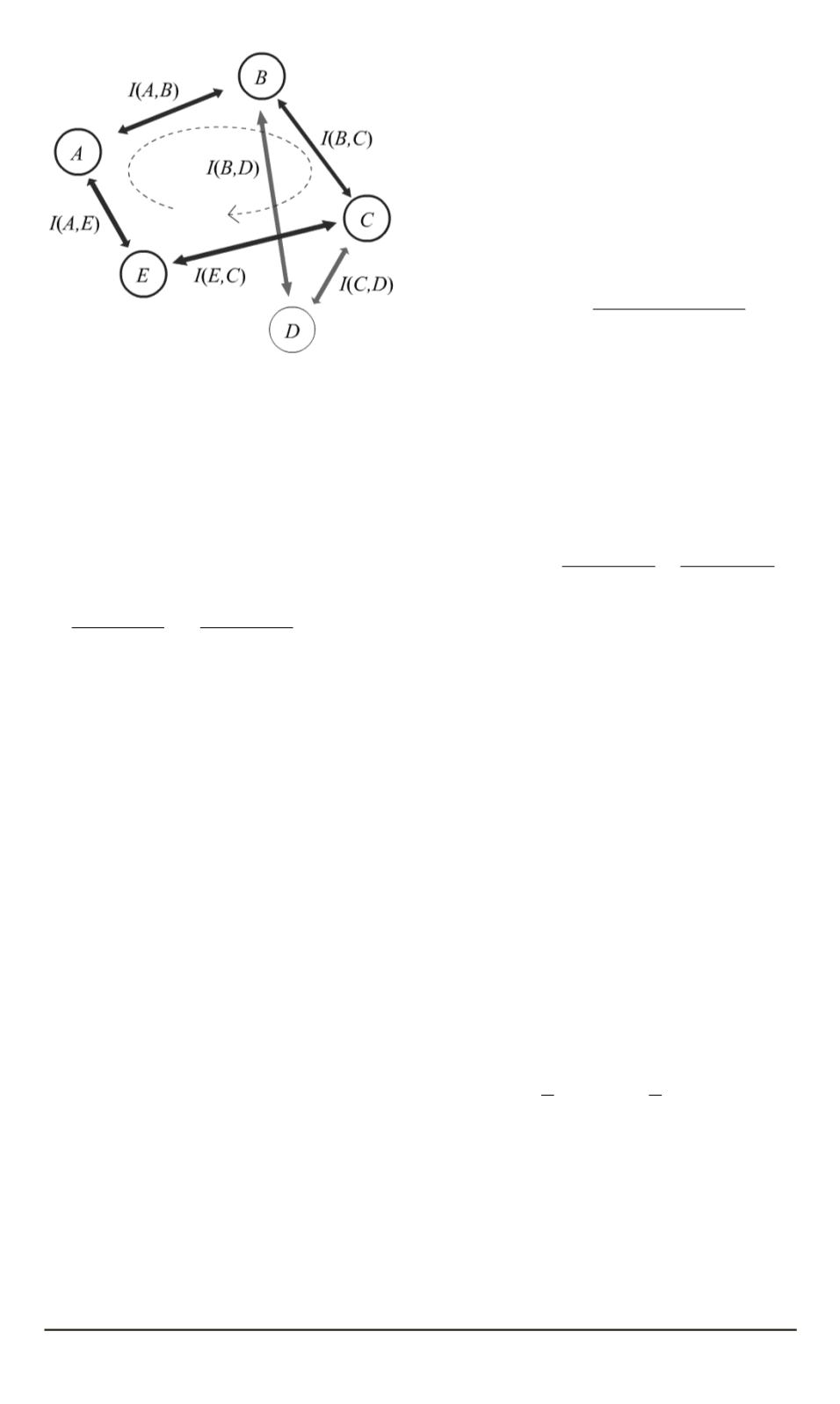
Рис. 2. Демонстрация циклического
свойства
c
2
в том смысле, что
I
(
X, Y
) =
=
I
(
Y, X
)
. Однако мера причинно-
сти антисимметрична:
c
2
(
X, Y
) =
=
−
c
2
(
Y, X
)
.
Кроме того, можно показать,
что выражение (1) может быть пе-
реписано в виде
c
2
(
X, Y
) =
I
(
X, Y
)
S
(
X
)
−
S
(
Y
)
.
Тогда, если выбрать некоторый за-
мкнутый контур, который соеди-
няет некоторое подмножество этих
систем, направление обхода этого
контура и рассчитать сумму всех величин взаимной информации, раз-
деленных на соответствующие значения
c
2
, то получим ноль. Напри-
мер, для контура
A
−
B
−
C
−
E
(см. рис. 2) имеем
I
(
A, B
)
c
2
(
A, B
)
+
I
(
B, C
)
c
2
(
B, C
)
+
+
I
(
C, E
)
c
2
(
C, E
)
+
I
(
A, E
)
c
2
(
E, A
)
= 0
. Можно интерпретировать это тождество
как запрет на существование замкнутых причинных контуров.
Применение причинного анализа к телепортации.
Теперь мож-
но рассмотреть применение причинного анализа к телепортации. В
первую очередь рассмотрим подход, использующий тензорные произ-
ведения. С его позиции телепортация происходит в момент белловско-
го измерения. Рассмотрим две конфигурации эксперимента. В случае,
приведенном на рис. 3,
a
, Боб измеряет свою частицу
B
до момента
измерения Алисы. С позиции тензорного подхода он просто получа-
ет некоторый случайный результат. В случае, представленном рис. 3,
б
,
Боб измеряет свою частицу после измерения, выполненного Алисой, и
следовательно, получает некоторый зашифрованный вариант входного
состояния Алисы.
Введем два варианта входного сигнала: I — это чистое состояние
|
0
i
; II — максимально смешанное состояние
1
2
|
0
ih
0
|
+
1
2
|
1
ih
1
|
. Итак,
получаем четыре различных конфигурации
a
I,
a
II,
b
I и
b
II.
Для выявления поведения причинности запишем матрицу плотно-
сти для полной системы
ACB
в виде функции параметра
p
. При
p
= 0
будем иметь системы в момент перед белловским измерением,
p
= 1
будет соответствовать моменту сразу после белловского измерения. В
результате получим четыре матрицы плотности во время белловского
30
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 6


