
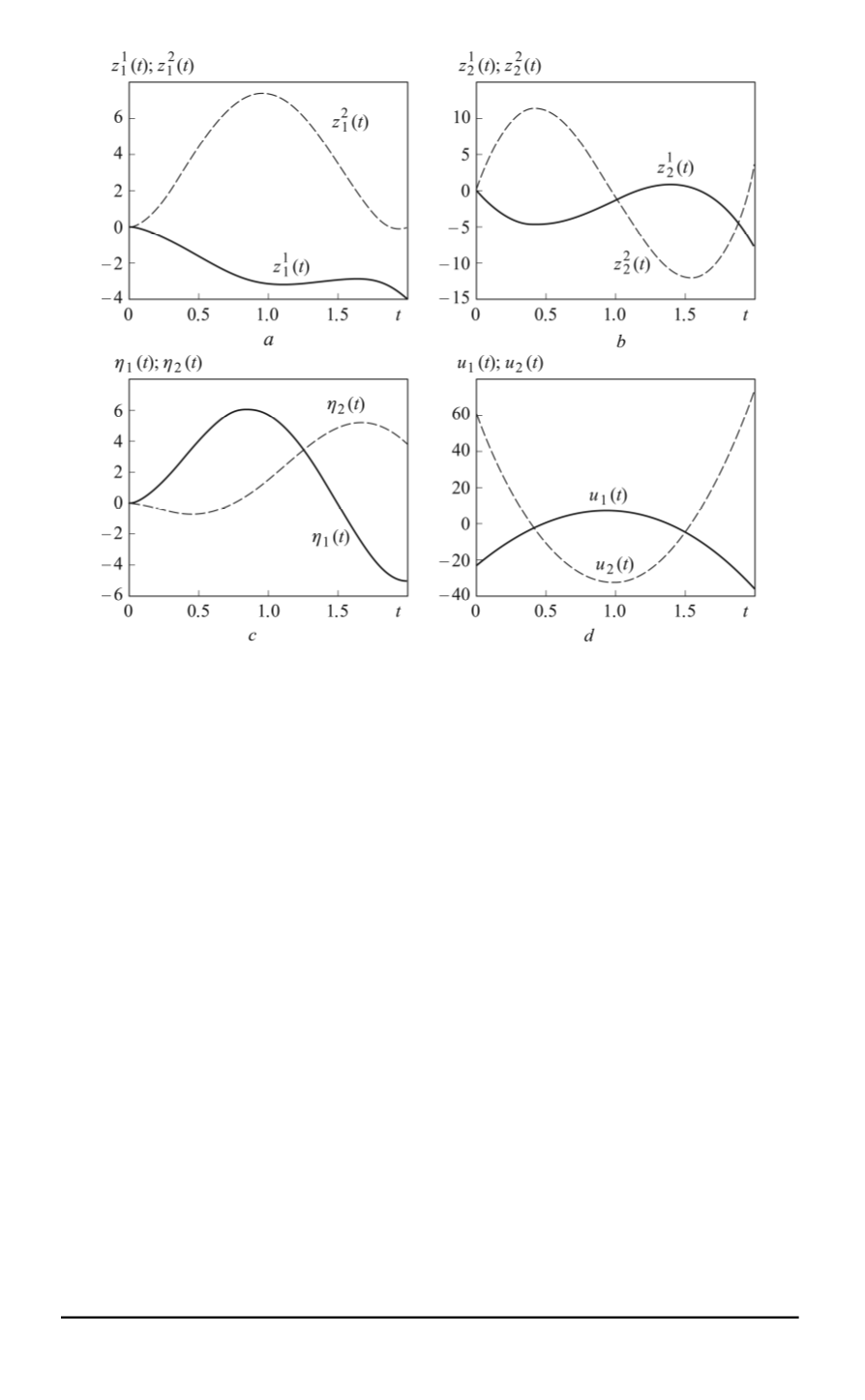
Functions
z
1
1
(
t
)
,
z
2
1
(
t
)
(
а
),
z
1
2
(
t
)
,
z
2
2
(
t
)
(
b
),
η
1
(
t
)
,
η
2
(
t
)
(
c
), and
u
1
(
t
)
,
u
2
(
t
)
(
d
)
the system can be transformed to a regular quasicanonical form. Along
with this, the terminal problem for the initial system is transformed to the
equivalent terminal problem for the system of a quasicanonical form. For
a quasicanonical system, the sufficient condition of the existence of the
terminal problems solution is proved. A method for solving the terminal
tasks is proposed on the basis of this condition. An example is given of
the terminal task solution development using the method proposed for the
sixth-order system.
The work was supported by the Russian Foundation for Basic Research
(
grants 14-07-00813, 13-07-00736
)
.
REFERENCES
[1] Krasnoshchechenko V.I., Krishchenko A.P. Nelineynye sistemy: geometricheskie
metody analiza i sinteza [Nonlinear systems: geometric methods for analysis and
synthesis]. Moscow, MGTU im. N.E. Baumana Publ., 2005. 520 p.
[2] Elkin V.I. Reduktsiya nelineynykh upravlyaemykh sistem: differentsial’no
geometricheskiy podkhod [Reduction of nonlinear controlled systems: a differential
geometric approach]. Moscow, Nauka Publ., 1997. 320 p.
[3] Agrachev A.A., Sachkov Yu.L. Geometricheskaya teoriya upravleniya [Geometric
control theory]. Moscow, Fizmatlit Publ., 2005. 392 p.
ISSN 1812-3368. Herald of the BMSTU. Series “Natural Sciences”. 2014. No. 5
29

















