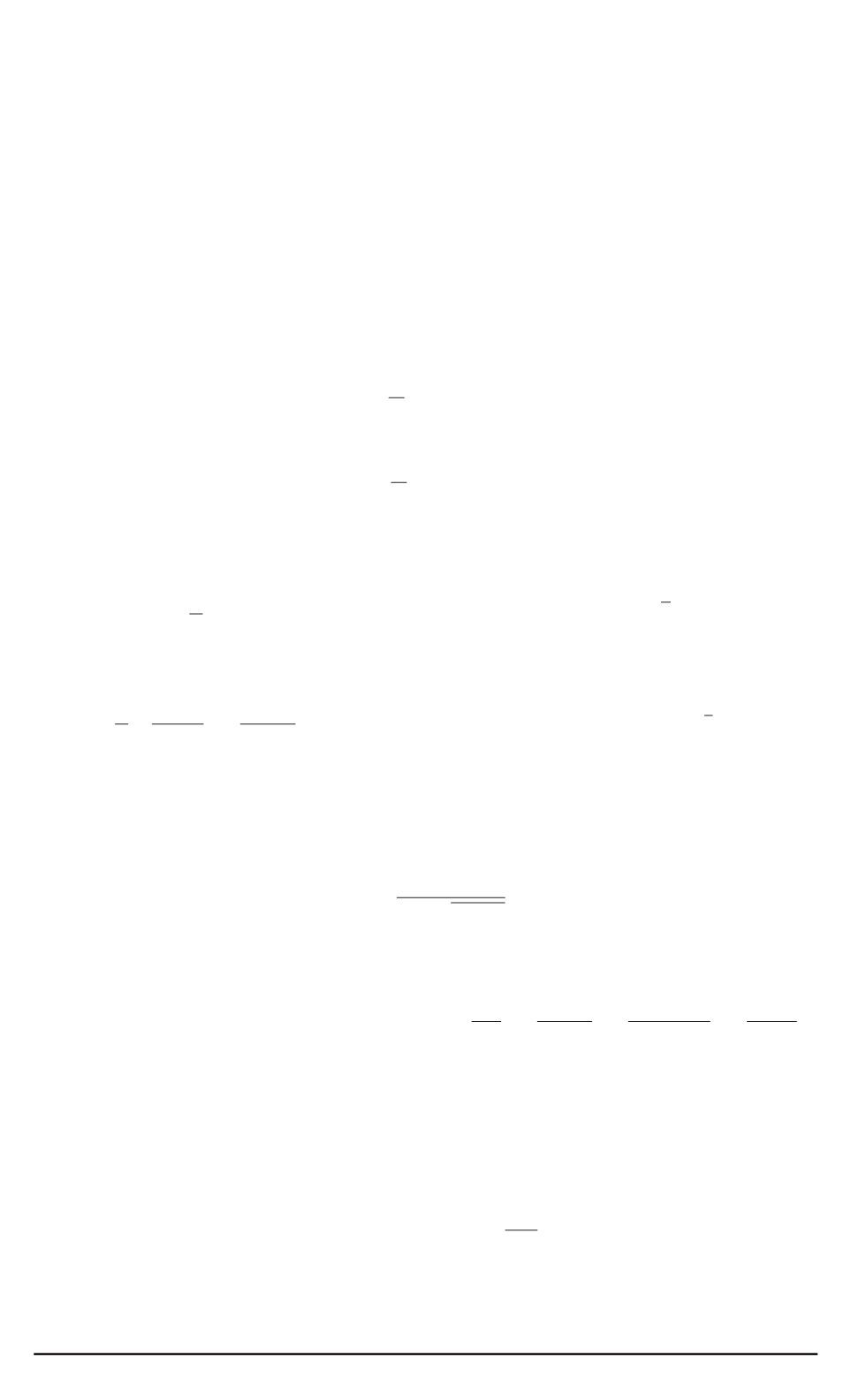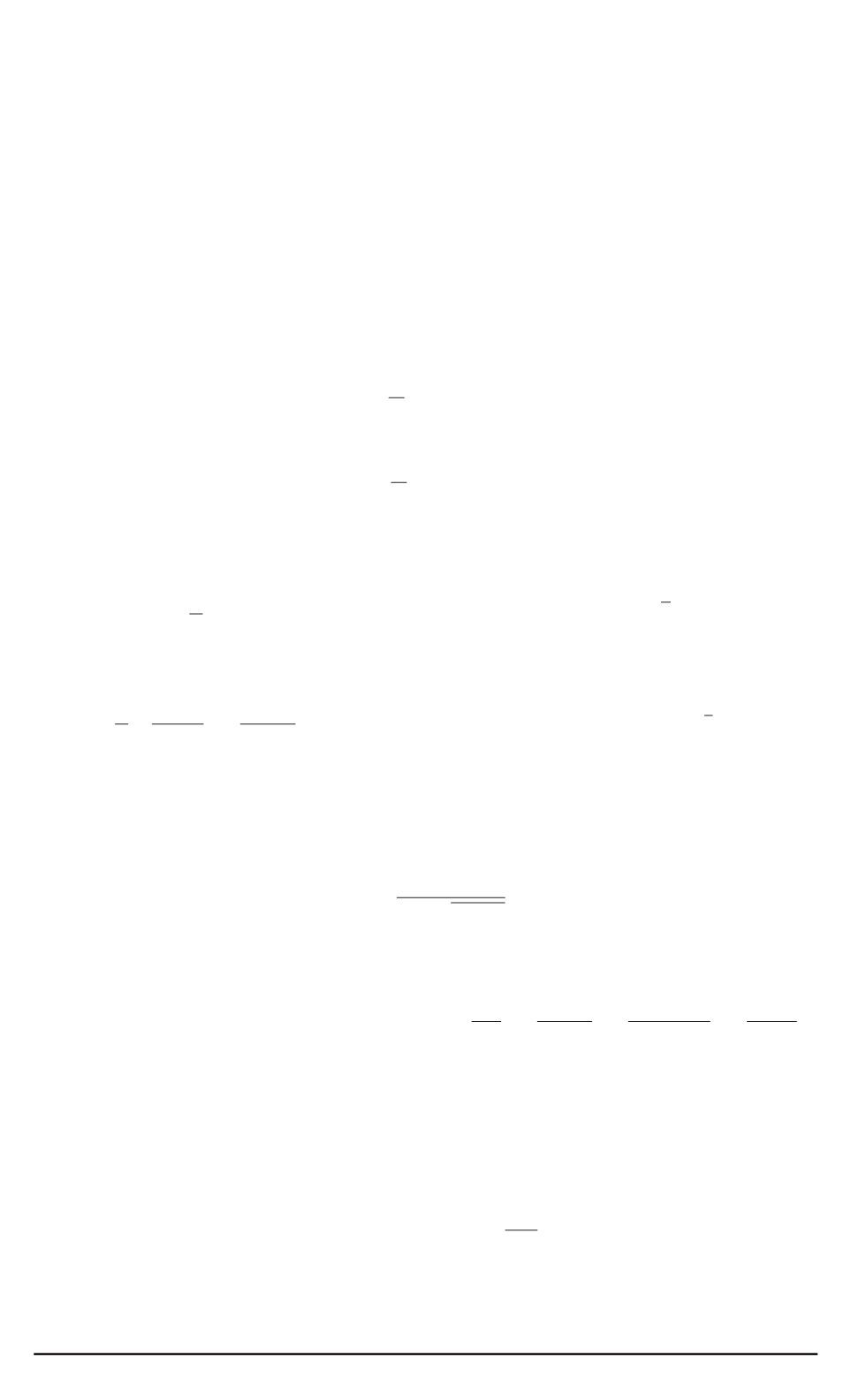
где
y
= 1
−
exp[
−
ρ
(
R
−
R
e
)]
;
R, R
e
— межъядерное и равновесное
межъядерное расстояния;
V
e
, ρ, b
n
— параметры потенциальной функ-
ции ВМ.
В средней части потенциальной кривой, которая представляет со-
бой экспериментально исследованный диапазон колебательных кван-
товых чисел, использован потенциал Ридберга–Клейна–Риса (РКР).
Потенциальная кривая РКР не имеет аналитического вида, она стро-
ится в виде набора классических поворотных точек
R
min
и
R
max
для
экспериментально изученных колебательных уровней энергии.
Для расчета поворотных точек потенциала РКР используются
функции
f
и
g
:
R
min
=
f
g
+
f
2
1
/
2
−
f
;
(2)
R
max
=
f
g
+
f
2
1
/
2
+
f.
(3)
Значения
f
и
g
определяются соотношениями
f
=
1
2
(
R
max
−
R
min
) =
k
v
v
=
v
min
[
G
(
v
)
−
G
(
v
)]
−
1
2
dv
;
(4)
g
=
1
2
1
R
min
−
1
R
max
=
k
−
1
v
v
=
v
min
B
(
v
)[
G
(
v
)
−
G
(
v
)]
−
1
2
dv ,
(5)
где
G
(
v
) =
m
n
=1
Y
n,
0
(
v
+ 0
,
5)
n
;
Y
n,
0
— коэффициенты Данхема;
B
(
v
)
—
вращательные постоянные;
k
=
h
2
π
2
hcμ
; значение нижнего предела
интегралов (4) и (5) находится из условия
E
(
v, J
= 0) =
G
(
v
) +
Y
00
= 0;
Y
00
=
B
e
4
+
α
e
ω
e
12
B
e
+
(
α
e
ω
e
)
2
144
B
3
e
−
ω
e
x
e
4
,
где
B
e
,
α
e
,
ω
e
,
ω
e
x
e
— экспериментальные вращательные и колебатель-
ные молекулярные постоянные.
Участок потенциальной кривой при больших значениях межъядер-
ного расстояния аппроксимирован функцией
U
(
R
) =
D
e
−
C
n
R
n
,
(6)
где
D
e
— экспериментальное значение энергии диссоциации;
C
n
—
параметры функции (6);
n
= 3
,
6
,
8
.
62
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2010. № 4