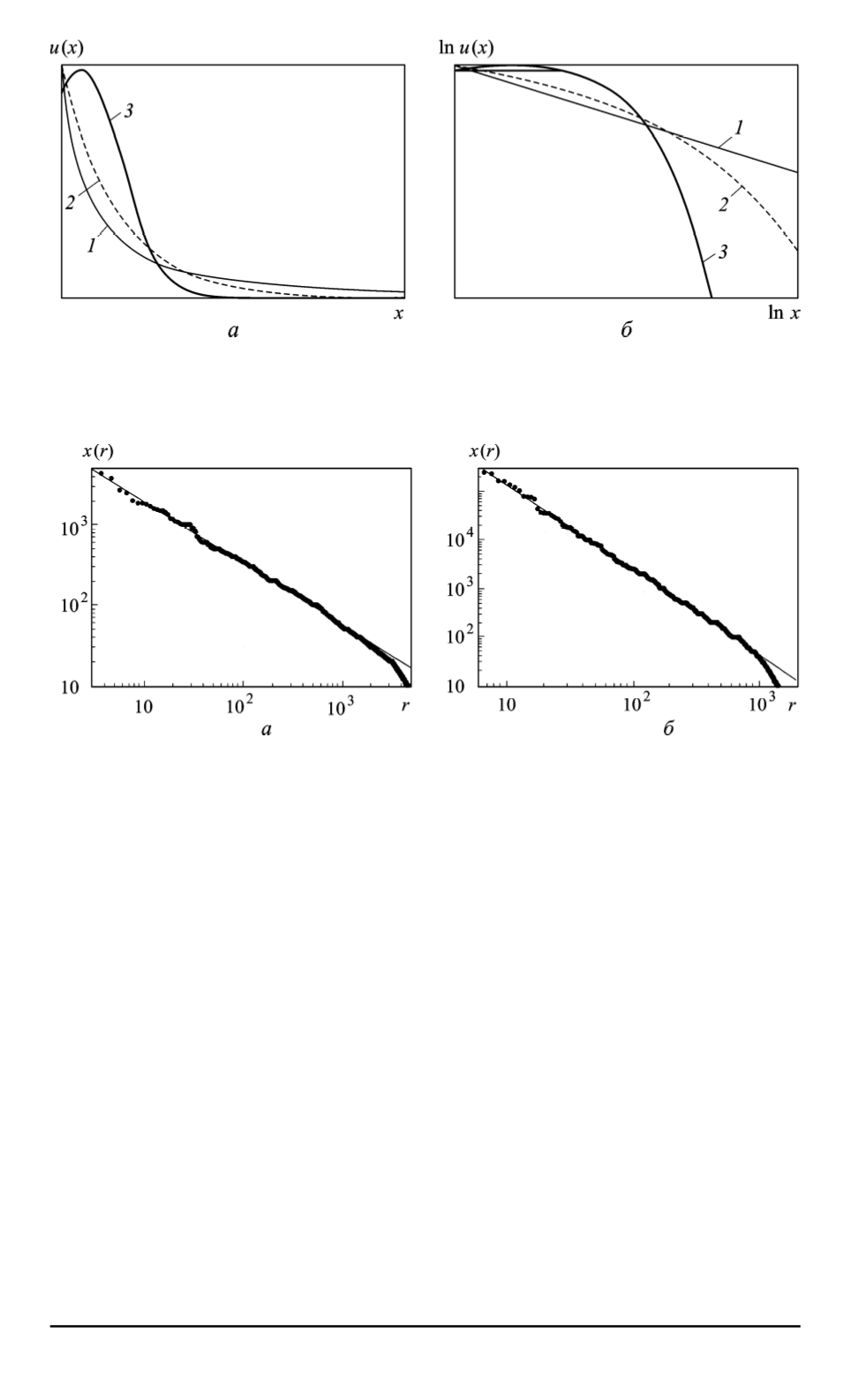
Рис. 1. Плотность вероятности нормального (
3
), экспоненциального (
1
) и сте-
пенного (
2
) распределений в линейном (
а
) и двойном логарифмическом (
б
) мас-
штабах
Рис. 2. Степенная статистика катастроф и бедствий (по данным работы [26] по
состоянию на 24.10.2003):
a
— ранжировка техногенных катастроф по числу погибших (2047 крупнейших со-
бытий описываются степенной зависимостью c
α
= 1
,
3
);
б
— ранжировка стихийных
бедствий по числу раненых (1084 события,
α
= 0
,
57
)
величиной. Можно показать, что при должном выборе
r
0
зависимость
величины события от присвоенного ему таким способом номера (ран-
га) выражается формулой
x
(
r
)
r
−
1/
α
(4)
в случае, если плотность вероятности имеет вид (3) на некотором от-
резке и равна нулю вне его. На рис. 2 приведены типичные зависимо-
сти ранг–размер, получаемые при анализе бедствий и катастроф (иде-
альным степенным зависимостям в двойном логарифмическом мас-
штабе соответствуют прямые).
В случае степенных распределений крупные события, со значи-
мой вероятностью происходящие в системе, могут на много порядков
превосходить типичные события, мерой которых является среднее. А
при
α <
1
сумма выборочных значений оказывается соизмеримой с
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2009. № 1
69


